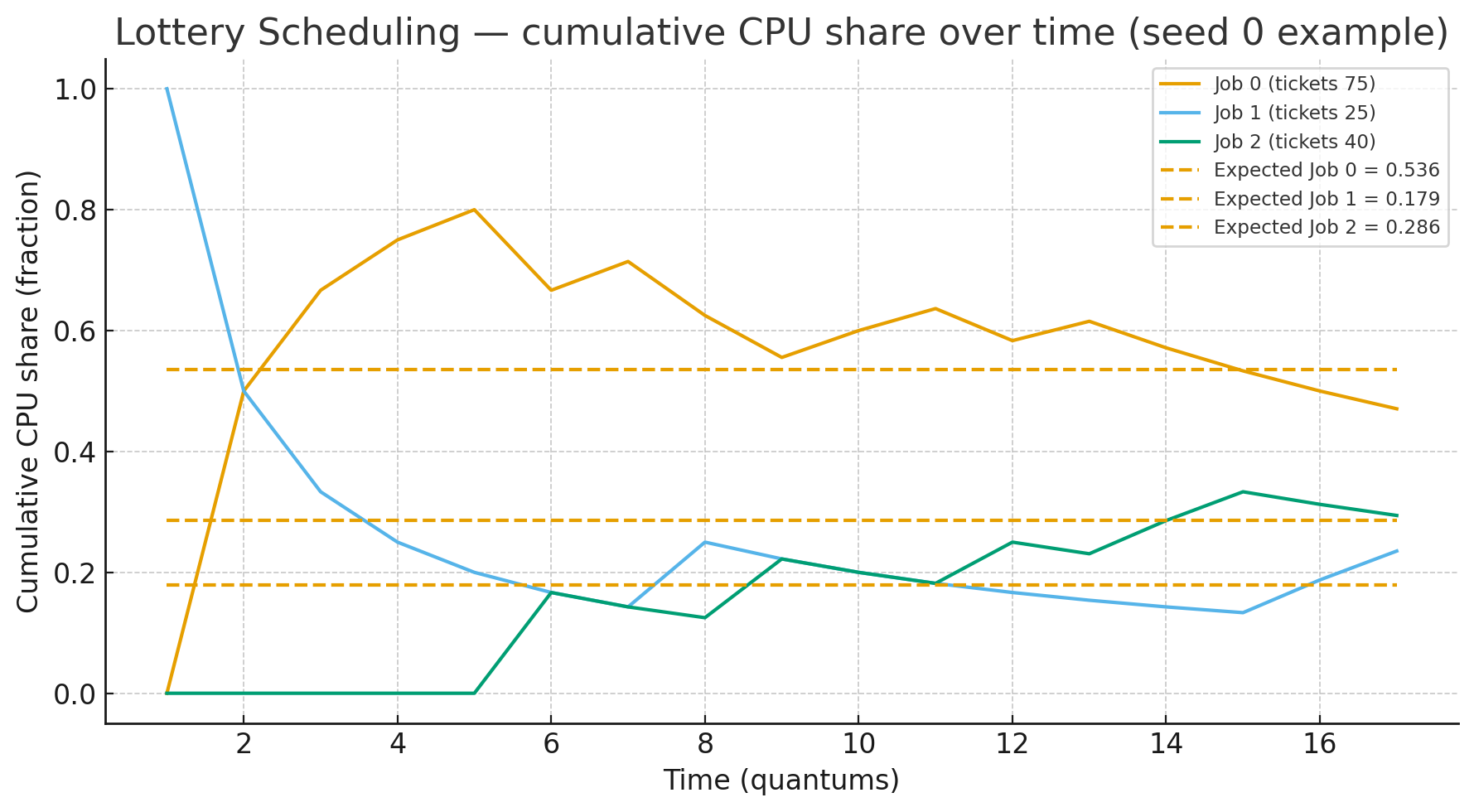
-
root@C202511211157657:~# tar xvzf HW-Lottery.tgz ./._lottery.py lottery.py ./._README-lottery README-lottery root@C202511211157657:~# python3 lottery.py ARG jlist ARG jobs 3 ARG maxlen 10 ARG maxticket 100 ARG quantum 1 ARG seed 0 Here is the job list, with the run time of each job: Job 0 ( length = 8, tickets = 75 ) Job 1 ( length = 4, tickets = 25 ) Job 2 ( length = 5, tickets = 40 ) Here is the set of random numbers you will need (at most): Random 783799 Random 303313 Random 476597 Random 583382 Random 908113 Random 504687 Random 281838 Random 755804 Random 618369 Random 250506 Random 909747 Random 982786 Random 810218 Random 902166 Random 310147 Random 729832 Random 898839
To get the result, just need to do modular operation to these random numbers and see which range they would fall in.
Using Excel to finish some dull opreations for you is highly recommended.
Notice that modular number will be updated when a job is finished.
| Time | Random Number | Total (Modular) | Result | Current JOB | NOTE |
|---|---|---|---|---|---|
| 1 | 783799 | 140 | 79 | JOB1 | |
| 2 | 303313 | 140 | 73 | JOB0 | |
| 3 | 476597 | 140 | 37 | JOB0 | |
| 4 | 583382 | 140 | 2 | JOB0 | |
| 5 | 908113 | 140 | 73 | JOB0 | |
| 6 | 504687 | 140 | 127 | JOB2 | |
| 7 | 281838 | 140 | 18 | JOB0 | |
| 8 | 755804 | 140 | 84 | JOB1 | |
| 9 | 618369 | 140 | 129 | JOB2 | |
| 10 | 250506 | 140 | 46 | JOB0 | |
| 11 | 909747 | 140 | 27 | JOB0 | |
| 12 | 982786 | 140 | 126 | JOB2 | |
| 13 | 810218 | 140 | 38 | JOB0 | JOB0 DONE AT TIME 13 |
| 14 | 902166 | 65 | 31 | JOB2 | |
| 15 | 310147 | 65 | 32 | JOB2 | JOB2 DONE AT TIME 15 |
| 16 | 729832 | 40 | 32 | JOB1 | |
| 17 | 898839 | 40 | 39 | JOB1 | JOB2 DONE AT TIME 17 |
Actually:
Correct.
root@C202511211157657:~# python3 lottery.py -s 1
ARG jlist
ARG jobs 3
ARG maxlen 10
ARG maxticket 100
ARG quantum 1
ARG seed 1
Here is the job list, with the run time of each job:
Job 0 ( length = 1, tickets = 84 )
Job 1 ( length = 7, tickets = 25 )
Job 2 ( length = 4, tickets = 44 )
Here is the set of random numbers you will need (at most):
Random 651593
Random 788724
Random 93859
Random 28347
Random 835765
Random 432767
Random 762280
Random 2106
Random 445387
Random 721540
Random 228762
Random 945271| Time | Random Number | Total (Modular) | Result | Current JOB | NOTE |
|---|---|---|---|---|---|
| 1 | 651593 | 153 | 119 | JOB2 | |
| 2 | 788724 | 153 | 9 | JOB0 | JOB0 Finished at Time 2 |
| 3 | 93859 | 69 | 19 | JOB1 | |
| 4 | 28347 | 69 | 57 | JOB2 | |
| 5 | 835765 | 69 | 37 | JOB2 | |
| 6 | 432767 | 69 | 68 | JOB2 | JOB2 Finished at Time 6 |
| 7 | 762280 | 25 | 5 | JOB1 | |
| 8 | 2106 | 25 | 6 | JOB1 | |
| 9 | 445387 | 25 | 12 | JOB1 | |
| 10 | 721540 | 25 | 15 | JOB1 | |
| 11 | 228762 | 25 | 12 | JOB1 | |
| 12 | 945271 | 25 | 21 | JOB1 | JOB1 Finished at Time 12 |
Actually: Correct.
-
root@C202511211157657:~# python3 lottery.py -l 10:1,10:100 ARG jlist 10:1,10:100 ARG jobs 3 ARG maxlen 10 ARG maxticket 100 ARG quantum 1 ARG seed 0 Here is the job list, with the run time of each job: Job 0 ( length = 10, tickets = 1 ) Job 1 ( length = 10, tickets = 100 ) Here is the set of random numbers you will need (at most): Random 844422 Random 757955 Random 420572 Random 258917 Random 511275 Random 404934 Random 783799 Random 303313 Random 476597 Random 583382 Random 908113 Random 504687 Random 281838 Random 755804 Random 618369 Random 250506 Random 909747 Random 982786 Random 810218 Random 902166
| Time | Random Number | Total (Modular) | Result | Current JOB | NOTE |
|---|---|---|---|---|---|
| 1 | 844422 | 101 | 62 | JOB1 | |
| 2 | 757955 | 101 | 51 | JOB1 | |
| 3 | 420572 | 101 | 8 | JOB1 | |
| 4 | 258917 | 101 | 54 | JOB1 | |
| 5 | 511275 | 101 | 13 | JOB1 | |
| 6 | 404934 | 101 | 25 | JOB1 | |
| 7 | 783799 | 101 | 39 | JOB1 | |
| 8 | 303313 | 101 | 10 | JOB1 | |
| 9 | 476597 | 101 | 79 | JOB1 | |
| 10 | 583382 | 101 | 6 | JOB1 | JOB1 Finished at Time 10 |
| 11 | 908113 | 1 | 0 | JOB0 | |
| 12 | 504687 | 1 | 0 | JOB0 | |
| 13 | 281838 | 1 | 0 | JOB0 | |
| 14 | 755804 | 1 | 0 | JOB0 | |
| 15 | 618369 | 1 | 0 | JOB0 | |
| 16 | 250506 | 1 | 0 | JOB0 | |
| 17 | 909747 | 1 | 0 | JOB0 | |
| 18 | 982786 | 1 | 0 | JOB0 | |
| 19 | 810218 | 1 | 0 | JOB0 | |
| 20 | 902166 | 1 | 0 | JOB0 | JOB0 Finished at Time 20 |
Actually: correct.
The response time and wait time for job0 is way longer than job1 due to the unbalance proportion of lotteries.
U = 10 / 20 = 0.5, which is pretty unfair.
JOB0 didn’t have any (or few, as I am not lucky enough) chance to execute its task.
-
root@C202511211157657:~# python3 lottery.py -l 100:100,100:100 -s 1 -c ... Jobs: ( job:0 timeleft:4 tix:100 ) (* job:1 timeleft:1 tix:100 ) --> JOB 1 DONE at time 196 ... Jobs: (* job:0 timeleft:1 tix:100 ) ( job:1 timeleft:0 tix:--- ) --> JOB 0 DONE at time 200 root@C202511211157657:~# python3 lottery.py -l 100:100,100:100 -s 2 -c ... Jobs: ( job:0 timeleft:10 tix:100 ) (* job:1 timeleft:1 tix:100 ) --> JOB 1 DONE at time 190 ... Jobs: (* job:0 timeleft:1 tix:100 ) ( job:1 timeleft:0 tix:--- ) --> JOB 0 DONE at time 200 root@C202511211157657:~# python3 lottery.py -l 100:100,100:100 -s 3 -c ... Random 519015 -> Winning ticket 15 (of 200) -> Run 0 Jobs: (* job:0 timeleft:1 tix:100 ) ( job:1 timeleft:4 tix:100 ) --> JOB 0 DONE at time 196 ... Random 68067 -> Winning ticket 67 (of 100) -> Run 1 Jobs: ( job:0 timeleft:0 tix:--- ) (* job:1 timeleft:1 tix:100 ) --> JOB 1 DONE at time 200U = (196 + 190 + 196) / (200 * 3) = 0.97
So it would be pretty fair and balanced. -
Quantum increases -> step length increases -> number of steps decreases, thus, the degree of convergence decreases, and the fairness also decreases.
-